报 告 人： 秦厚荣 教授
报告题目：Congruent numbers, quadratic forms and algebraic K-theory
报告时间：2019年11月16日
报告摘要： We show that if a square-free and odd (respectively, even) positive integer n is a congruent number, then
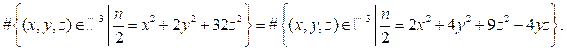respectively,
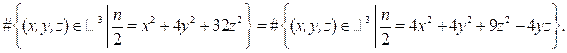If we assume that the weak
Brich-Swinnerton-Dyer conjecture is true for the elliptic curves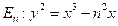 
, then, conversely, these equalities imply that n is a congruent number.
We shall also discuss some applications of the proposed method. In particular, for a prime p, we show that if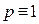 
(mod 8) is a congruent number, then the 8-rank of 
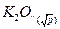equals one, and if 
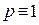(mod 16) with 
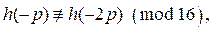then 2p is not a congruent number.